本文共 2065 字,大约阅读时间需要 6 分钟。
前段时间一直在研究OpenRCE的sulley框架,在艰难安装过程也顺便安装了pcapy,突然发现网上对pcapy的解释说明不是很全,所以在此整理和详细说明一下pcapy的安装过程,希望能帮助大家!测试环境是win 10 64位系统
安装pcapy所需的工具
- Python编译器,Versions 2.1.3 或以上,在这里我们使用的2.7.9
- 一个C++的编译器。GCC G++ 2.95,Microsoft Visual Studio 6.0同样可以,我们这里是用的MinGW来进行编译,一个windows专用的轻型编译器
- Libpcap 0.7.2 或以上,windows用户的话我们使用的是WinPcap 3.0或以上版本
- 最新发布的pcapy版本
Step 1 安装GCC编译器
在linux系统里面安装gcc编译器可以说很容易的,我们这里主要讲的是在windows下面安装gcc,主要用到的是MinGW。
MinGW,是Minimalist GNU for Windows的缩写。它是一个可自由使用和自由发布的Windows特定头文件和使用GNU工具集导入库的集合,允许你在GNU/Linux和Windows平台生成本地的Windows程序而不需要第三方C运行时(C Runtime)库。
有两种方式下载安装:| ,,如果您使用了第一种方式,在安装界面选择package里面勾选:1)mingw32-base - Base Package 2)mingw32-gcc-g++ - C++ Compiler 3)mingw32-gcc-objc - Objective-C Compiler
这里我们使用的是第二种方式,安装MinGW的过程和一般程序的安装过程一样,值得注意的是在勾选界面进行如图所示的选择就可以了: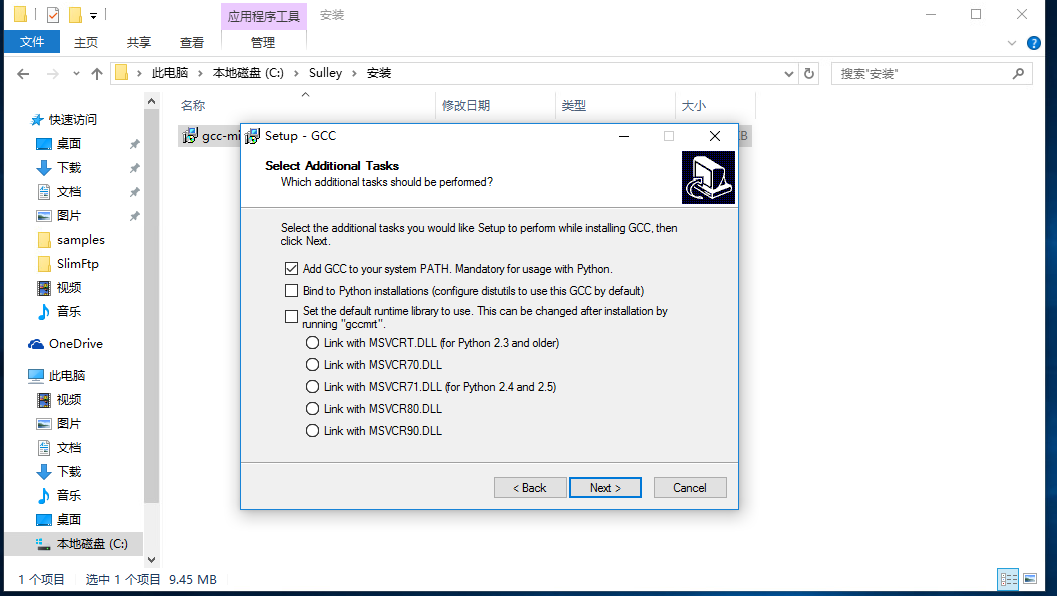
Step 2 下载和安装Git(可选)
这是可选的步骤,如果你下载了Git,那么获取github上面的项目会变得简单,因为后面的项目只会用到git clone这个命令;如果你没下载Git,那也没关系,在之后的git clone https://xxxxx.com命令直接打开https://xxxxx.com这个网站就行,然后点击右上角的download下载zip包就行啦。
Step 3 设置环境变量
接下来就是配置环境变量,使得git python MinGW命令能在cmd中使用,如图: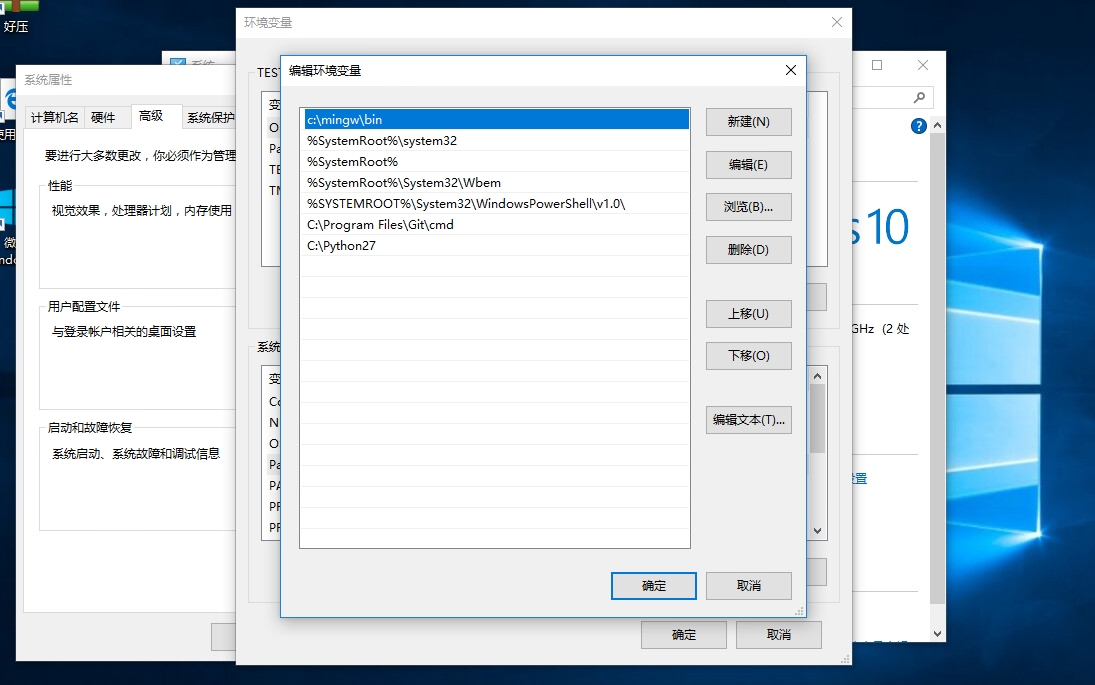
Step 4 下载Pcapy和WinPcap Dev Kit
git clone 和下载 (WinPcap开发者版本,主要使用到这里的头文件和lib),并把下载的WinPack放在c:\Sulley\目录下(当然你可以选择自己的方式)。
Step 5 编译安装pcapy
进入pcapy的目录,运行以下代码:
pcapy的目录>python setup.py build_ext -c mingw32 -I "C:\sulley\WpdPack\Include" -L "C:\sulley\WpdPack\Lib"(主要是包含这两个目录)running build_extbuilding 'pcapy' extensioncreating buildcreating build\temp.win32-2.7creating build\temp.win32-2.7\Releasecreating build\temp.win32-2.7\Release\win32...省略...pcapy的目录>python setup.py installrunning installrunning buildrunning build_extrunning install_libcopying build\lib.win32-2.7\pcapy.pyd -> C:\python27\Lib\site-packagesrunning install_datacreating C:\python27\sharecreating C:\python27\share\doccreating C:\python27\share\doc\pcapycopying README -> C:\python27\share\doc\pcapy...省略...
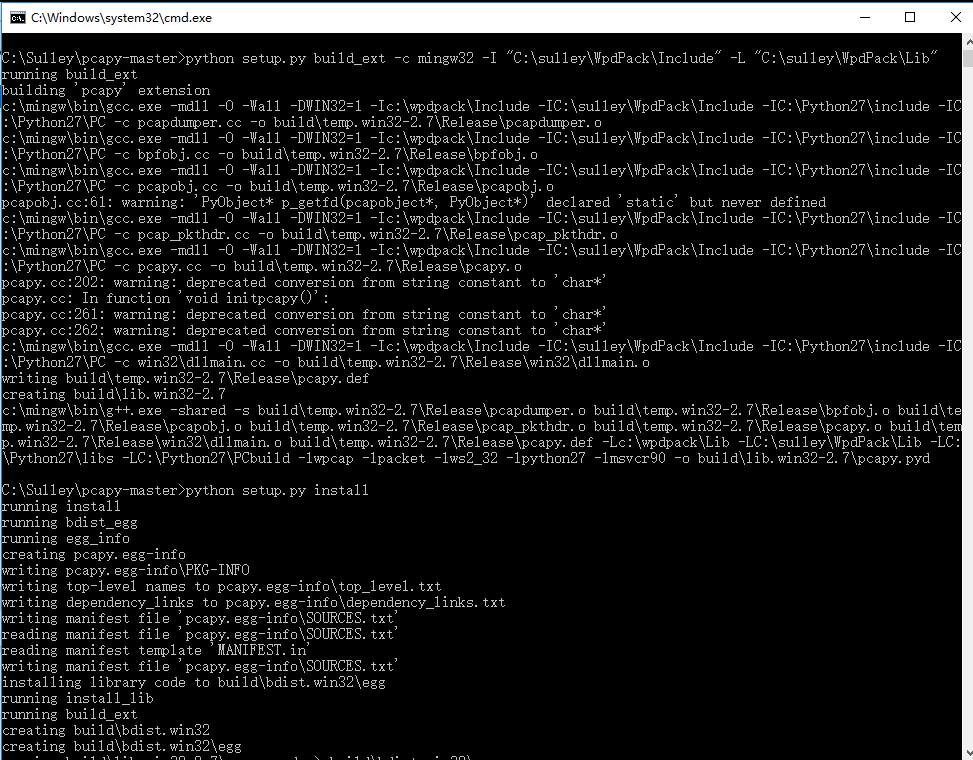
这里是非常容易出现错误的地方,如果出现了什么bug可以在底下评论,大家一起解决。
Step 6 下载和安装WinPcap
您是不是感觉已经安装完了呢,其实并没有,如果此时我们进Python命令行执行import pcapy命令会发现Import Error:DLL not fond错误,如图: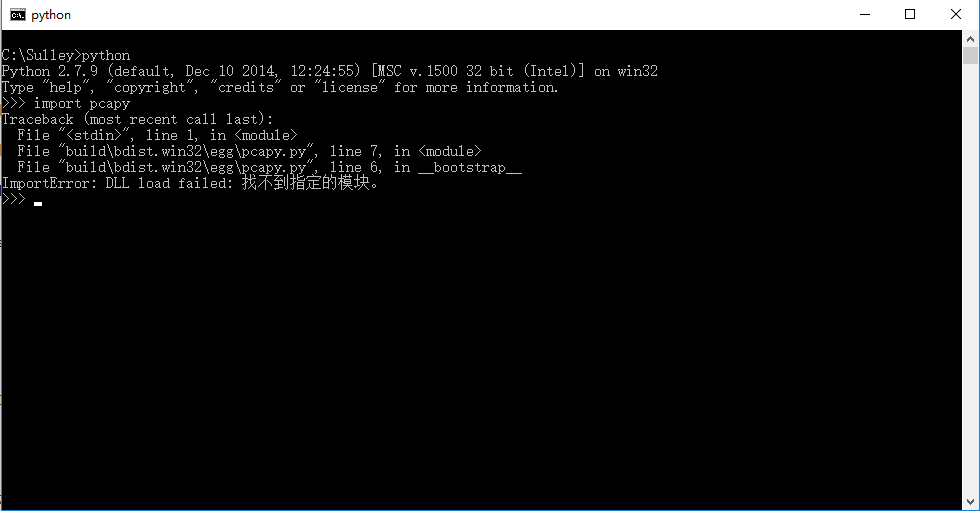
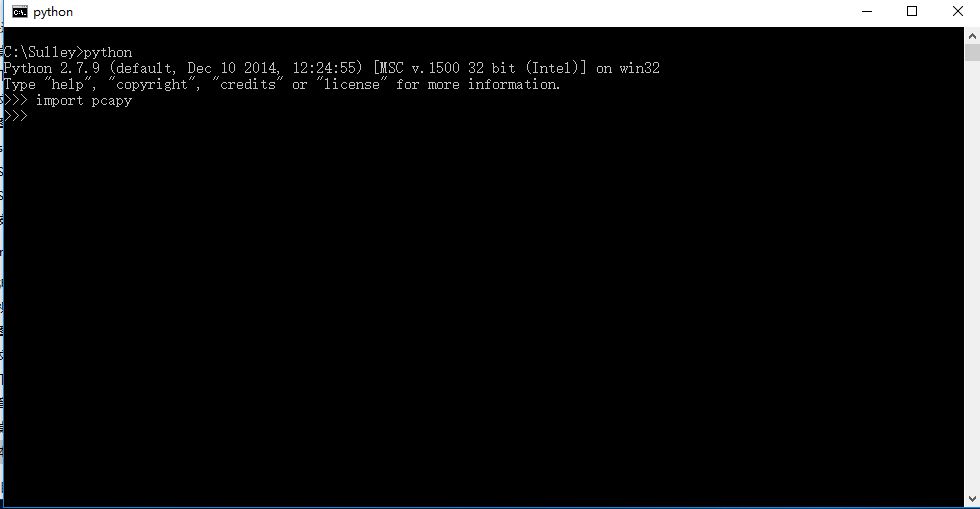
这是因为我们还没有安装WinPcap,这些DLL就缺失了,下载,然后进行安装(一直next就ok拉),最后我们再次运行一下import pcapy命令,就会发现没有任何问题啦,如图:
PS:在这里我提供安装pcapy所需的上述所有的安装包供大家下载,懒人必备:
转载地址:http://atjnz.baihongyu.com/